3  Estadística descriptiva

3.1 Objetivos de la sesión

• Tras familiarizarnos con los principios básicos de la programación en R y la manipulación de sus elementos clave, nos centraremos en examinar a fondo una base de datos. Al concluir esta sesión, el estudiante dominará las técnicas y métodos estadísticos esenciales para sintetizar y destacar las características principales de un conjunto de datos.

3.2 Presentación

3.3 Problema de investigación y data

Disponemos de una base de datos que incluye una variedad de indicadores e índices para 95 países alrededor del mundo. Los datos abarcan:

-País

-Continente

-Región

-Índice

-Índice de Lavado de Activos

-Matrícula

-PBI per cápita

-Pobreza Urbano

-Gasto en educación

-Índice de Percepción de la Corrupción

-Estado de derecho

-Índice de Democracia

-Categoría del Índice de Democracia

-Índice de Crimen Organizado

library(tidyverse)
library(readxl)
data<-read_xlsx("data/AML.xlsx")

Veamos la data rápidamente:

head(data)

# A tibble: 6 × 14
  Pais       Continent Region AML_Index Matricula  PBIPC Pobreza URBANO gastoedu
  <chr>      <chr>     <chr>  <chr>         <dbl>  <dbl>   <dbl>  <dbl>    <dbl>
1 Afghanist… Asia      South… No se de…      50.1   552.    54.5   26       4.06
2 Albania    Europe    Centr… 4.75           86.6  5224.    14.3   62.1     2.47
3 Angola     Africa    Centr… 7.03           11.3  3437.    36.6   66.8     3.42
4 Argentina  Americas  South… No se de…      90.8 11688.    25.7   92.1     5.46
5 Armenia    Asia      Centr… 4.72           87.7  4212.    32     63.3     2.71
6 Austria    Europe    Weste… 4.099999…      87   51230.     3     58.7     5.5 
# ℹ 5 more variables: CPI_Index <dbl>, Rule_of_Law <dbl>,
#   Democracy_Index <dbl>, Democracy_Index_cat <chr>,
#   Organized_Crime_Index <dbl>

3.4 Estadísticos descriptivos

Además de memorizar las fórmulas, que sin duda son esenciales, te invito a que, al abordar una base de datos, consideres las siguientes preguntas esenciales al momento de describir una variable:

• ¿Cuál sería el mejor representante de estos datos?

• ¿Cuánto varían estos datos?

3.4.1 ¿Cuál sería el mejor representante de estos datos?

El “mejor representante” de un conjunto de datos se refiere a la medida de tendencia central que mejor resume la información de dicho conjunto. Las opciones principales incluyen la media, la mediana y la moda:

3.4.1.1 La media

La media es el promedio aritmético y proporciona un centro de gravedad de los datos. Es útil cuando los datos son simétricos y sin valores atípicos significativos. Recordemos que la función a utilizar es mean().

Por ejemplo, si deseamos la media de PBI per cápita, Pobreza y el Gasto de Educación:

mean(data$PBIPC)

[1] 11823.83

mean(data$Pobreza)

[1] 27.92947

mean(data$gastoedu)

[1] 4.427158

Si lo queremos ver de forma comparativa y en una sola línea de código podemos utilizar tidyverse:

data |> 
  summarise(mean(PBIPC), mean(Pobreza), mean(gastoedu))

# A tibble: 1 × 3
  `mean(PBIPC)` `mean(Pobreza)` `mean(gastoedu)`
          <dbl>           <dbl>            <dbl>
1        11824.            27.9             4.43

3.4.1.2 La mediana

La mediana es el valor que se encuentra en el punto medio de un conjunto de datos ordenado. Resulta especialmente informativa en distribuciones sesgadas, ya que no es tan susceptible a los valores extremos como la media. Usamos la función median().

Sigamos con las variables PBI per cápita, Pobreza y el Gasto de Educación:

median(data$PBIPC)

[1] 4900.76

median(data$Pobreza)

[1] 23.4

median(data$gastoedu)

[1] 4.56

Si lo queremos ver de forma comparativa podemos utilizar tidyverse:

data |> 
  summarise(median(PBIPC), median(Pobreza), median(gastoedu))

# A tibble: 1 × 3
  `median(PBIPC)` `median(Pobreza)` `median(gastoedu)`
            <dbl>             <dbl>              <dbl>
1           4901.              23.4               4.56

3.4.1.3 La moda

La moda es el valor o valores que aparecen con mayor frecuencia. Es la única medida de tendencia central aplicable a datos nominales. Para este caso en específico, podemos utilizar la función table() o también la función count() dentro de un fraseo de tidyverse:

table(data$Continent)

  Africa Americas     Asia   Europe  Oceania 
      29       20       17       26        3 

O también:

data |> 
  count(Continent)

# A tibble: 5 × 2
  Continent     n
  <chr>     <int>
1 Africa       29
2 Americas     20
3 Asia         17
4 Europe       26
5 Oceania       3

Podemos añadir también una columna de porcentaje usando la función mutate():

data |> 
  count(Continent) |> 
  mutate(Porcentaje=n/sum(n)*100)

# A tibble: 5 × 3
  Continent     n Porcentaje
  <chr>     <int>      <dbl>
1 Africa       29      30.5 
2 Americas     20      21.1 
3 Asia         17      17.9 
4 Europe       26      27.4 
5 Oceania       3       3.16

3.4.2 ¿Cuánto varían estos datos?

La variación de los datos se refiere al grado en que los valores del conjunto de datos difieren de una medida de tendencia central. Las medidas de variabilidad incluyen el rango, la varianza, la desviación estándar y el coeficiente de variación:

3.4.2.1 El rango

El rango ofrece una visión general muy básica de la variabilidad, indicando la diferencia entre los valores más alto y más bajo.

Es una medida muy sencilla de calcular y proporciona una idea general de la variabilidad de los datos. Sin embargo, no toma en cuenta la distribución de los datos en el conjunto, lo que puede hacer que la medida sea menos informativa en ciertos casos.

Para ver el valor mínimo y máximo:

range(data$PBIPC)

[1]   293.96 82708.51

range(data$Pobreza)

[1]  2.6 72.3

range(data$gastoedu)

[1] 1.11 7.67

Para ver el rango:

max(data$PBIPC)-min(data$PBIPC)

[1] 82414.55

max(data$Pobreza)-min(data$Pobreza)

[1] 69.7

max(data$gastoedu)-min(data$gastoedu)

[1] 6.56

3.4.2.2 La varianza y la desviación estándar

La varianza es una medida de dispersión que indica qué tan dispersos están los datos con respecto a su media.

Se calcula como el promedio de los cuadrados de las diferencias entre cada valor y la media del conjunto. En otras palabras, indica cuán alejados están los valores individuales de la media. La varianza proporciona una idea de la variabilidad o volatilidad de los datos, siendo un indicador clave de cuánto tienden a variar los valores respecto a la media.

\[s^2 = \frac{1}{N-1}\sum_{i=1}^{N}(x_i - \mu)^2\]

Advertencia

Se utiliza n−1 para calcular la varianza en una muestra como un ajuste para corregir el sesgo en la estimación de la varianza poblacional, garantizando una estimación más precisa. Esto lo entenderemos mejor cuando veamos inferencia.

La varianza proporciona una idea de la dispersión general de los datos, pero debido a que las diferencias se elevan al cuadrado, la varianza no está en las mismas unidades que los datos originales, lo que puede dificultar su interpretación directa.

Usamos la función var():

var(data$PBIPC)

[1] 276058288

var(data$Pobreza)

[1] 283.7038

var(data$gastoedu)

[1] 1.859397

Por otro lado, la desviación estándar, al tomar la raíz cuadrada de la varianza vuelve a las unidades originales de los datos, lo que facilita su comprensión e interpretación. La desviación estándar indica cuánto, en promedio, se desvían los valores de la media del conjunto de datos. Lo calculamos con la función sd().

Un valor bajo de desviación estándar indica que los datos están agrupados cerca de la media, mientras que un valor alto señala que los datos están más dispersos.

Sirve mucho cuando comparamos dos variables que están en las mismas unidades, como por ejemplo:

data |> filter(Continent=="Africa") |> summarise(sd(PBIPC))

# A tibble: 1 × 1
  `sd(PBIPC)`
        <dbl>
1       3509.

data |> filter(Continent=="Europe") |> summarise(sd(PBIPC))

# A tibble: 1 × 1
  `sd(PBIPC)`
        <dbl>
1      20462.

En este caso podemos evidenciar que en el caso de los países de África existe más dispersión (3508.5 dólares de distancia de la media en promedio) que en Europa (20461.5 dólares de distancia de la media en promedio).

Advertencia

A pesar que en la descripción de una variable se suele preferir utilizar la desviación estándar por las características mencionadas, la varianza tiene propiedades matemáticas importantes que la hacen el centro de diversas técnicas inferenciales que veremos más adelante.

3.4.2.3 El coeficiente de variación

El coeficiente de variación (CV) es una medida estadística que describe la relación entre la desviación estándar (σ) y la media (μ) de un conjunto de datos, expresada como un porcentaje.

De forma sencilla, el coeficiente de variación indica cuán grande es la variabilidad de los datos en comparación con la media del conjunto.

\[CV = \left( \frac{s}{\mu} \right) \times 100\%\]

El coeficiente de variación es particularmente útil porque proporciona una medida de variabilidad relativa independiente de la escala de los datos, lo cual permite comparar la dispersión de dos o más conjuntos de datos que podrían tener diferentes unidades de medida o medias muy distintas (lo que podría distorsionar el análisis).

Si bien NO HAY UN CONSENSO en los umbrales para la interpretación, para este curso, utilizaremos los siguientes criterios:

• ]0%-10%]: Variabilidad baja

• ]10%-20%]: Variabilidad media

• Mayor a 20%: Variabilidad alta

Por ejemplo, en nuestro caso, ¿qué tanta variabilidad posee PBI per cápita, Pobreza y el Gasto de Educación? ¿Cuál presenta la mayor variabilidad?

cv_PBIPC <- sd(data$PBIPC) / mean(data$PBIPC) * 100
cv_Pobreza <- sd(data$Pobreza) / mean(data$Pobreza) * 100
cv_gastoedu <- sd(data$gastoedu) / mean(data$gastoedu) * 100

cv_PBIPC

[1] 140.5214

cv_Pobreza

[1] 60.30729

cv_gastoedu

[1] 30.80073

Con esta medida estandarizada es mucho mejor realizar la comparación y responder a la pregunta planteada.

3.4.3 Comparación en grupos

Es común querer explorar cómo los descriptivos estadísticos varían entre diferentes grupos o categorías dentro de un conjunto de datos. Para facilitar este tipo de análisis, el paquete dplyr de R ofrece la función group_by(), que permite agrupar los datos por una o más variables categóricas y luego calcular estadísticas descriptivas para cada grupo. Esta práctica es especialmente útil para entender las diferencias y similitudes entre grupos, ayudando en la toma de decisiones basada en datos y en la formulación de hipótesis para análisis más detallados.

data |> 
  group_by(Continent) |> 
  summarise(cv_PBIPC=sd(PBIPC) / mean(PBIPC) * 100,
            cv_Pobreza = sd(Pobreza) / mean(Pobreza) * 100,
            cv_gastoedu = sd(gastoedu) / mean(gastoedu) * 100)

# A tibble: 5 × 4
  Continent cv_PBIPC cv_Pobreza cv_gastoedu
  <chr>        <dbl>      <dbl>       <dbl>
1 Africa       159.        36.4        35.6
2 Americas     121.        48.0        25.5
3 Asia          81.3       67.3        32.7
4 Europe        70.1       47.4        24.2
5 Oceania       39.2       24.2        35.0

3.5 Visualización de datos

Dependiendo del tipo de variables que se analizan, las técnicas y herramientas de visualización varían. A continuación, se describen las aproximaciones recomendadas para visualizar datos, diferenciando entre variables categóricas y numéricas.

3.5.1 Cómo funciona ggplot2

ggplot2 es un popular paquete de visualización de datos para el lenguaje de programación R, basado en los principios de la “Gramática de Gráficos”. Esta filosofía de diseño permite a los usuarios construir gráficos complejos y estéticamente agradables a partir de componentes básicos de forma intuitiva y flexible. El núcleo de ggplot2 radica en su sistema de capas, donde cada gráfico se construye agregando capas que pueden incluir, entre otros, los datos, las estéticas (como color, forma y tamaño), los objetos geométricos (como puntos, líneas y barras), las escalas, y las anotaciones. Este enfoque modular no solo facilita la personalización y optimización de los gráficos sino que también promueve una estructura de código clara y comprensible.

Vamos a hacer un ejemplo paso a paso:

1. Datos: Conjunto de datos a visualizar

Nuestra primera capa siempre va a ser la data. Sobre esta iniciamos la función ggplot y corroboramos que tenemos un lienzo en blanco.

data |> 
  ggplot()

2. Estéticas: Diseño básico del gráfico (Aesthetics)

Mapeo de variables a propiedades visuales como color, forma o tamaño, definidas con aes().

A diferencia del lienzo en blanco, ya contamos con un diseño. En este caso, hemos indicado al R que el eje X será la variable Pobreza.

data |> 
  ggplot()+
  aes(x=Pobreza)

Advertencia

En ggplot2, las capas de un gráfico se van adicionando secuencialmente utilizando el operador +.

3. Geometrías (Geoms) Representaciones gráficas de los datos, como puntos, líneas o barras (geom_point(), geom_line(), geom_bar(), etc.).

En nuestro ejemplo, podemos agregar la geometría de histograma:

data |> 
  ggplot()+
  aes(x=Pobreza)+
  geom_histogram()

`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.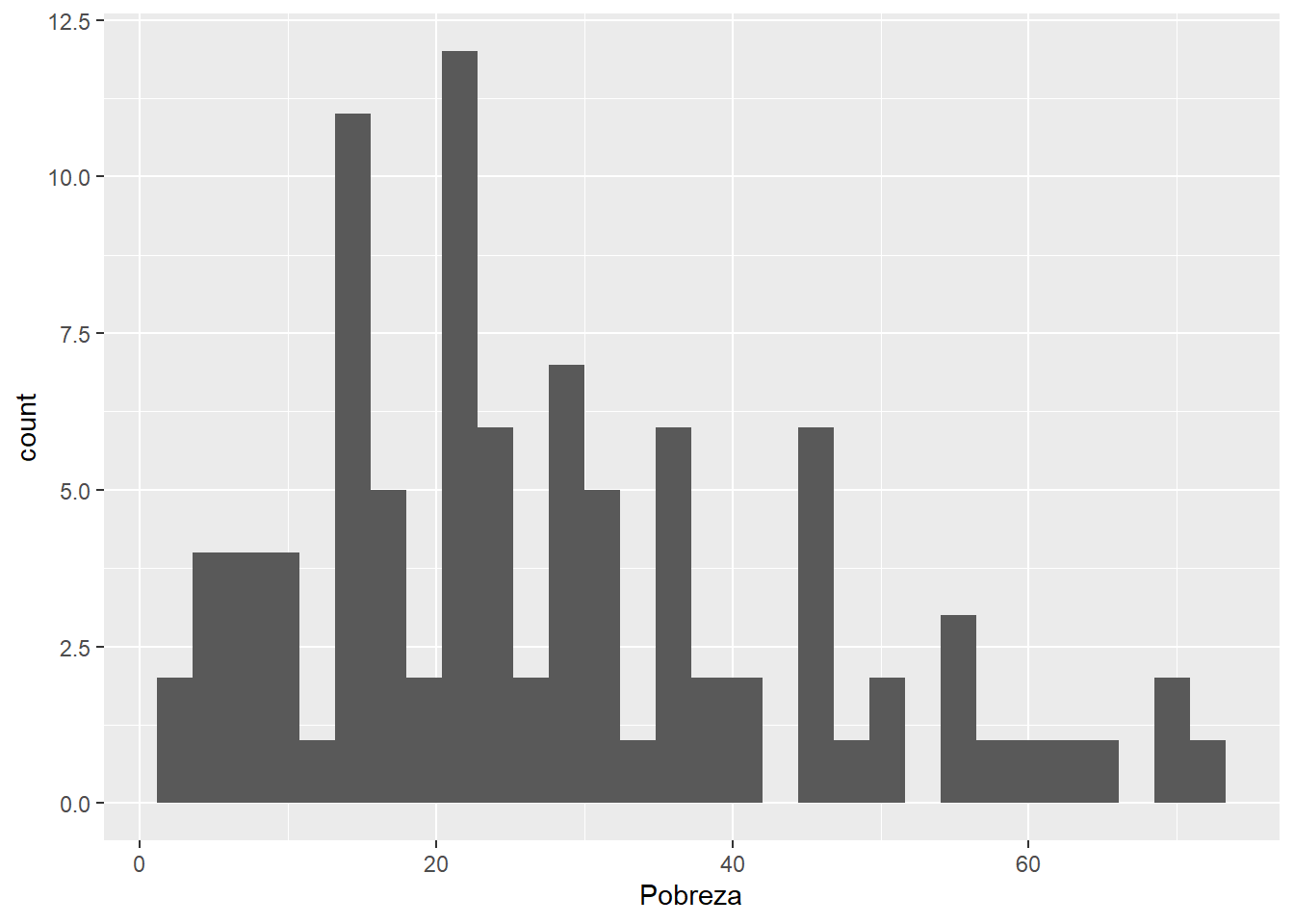

Nota

En el paquete {ggplot2} existen 30 geometrías disponibles. Puedes ver el detalle de estos en la documentación del paquete.

Esta estructura de capas hace que ggplot2 sea extremadamente poderoso para explorar y presentar datos de manera efectiva, permitiendo a los usuarios desde principiantes hasta expertos crear visualizaciones de datos complejas y personalizadas con relativa facilidad.

4. Facetas, Estadísticas, Coordenadas y Temas

Las demás capas del ggplot lo vamos a ir viendo a medida que vayamos avanzando en el curso. No obstante, te sugiero ver el siguiente ppt que profundiza y ejemplifica cada una de las capas restantes.

Si deseas adelantar un poco, puedes mirar esta presentación, donde exploro el detalle de las capas restantes.

También te sugiero ver este video de soporte

3.5.2 Para variables categóricas

3.5.2.1 Gráfico de barras

En un gráfico de barras vertical,las categorías se representan en el eje horizontal y la frecuencia o cantidad en el eje vertical.

El gráfico de barras es una herramienta útil para comparar la frecuencia o cantidad de diferentes categorías o variables en un conjunto de datos.

Utilizamos la función geom_bar(). El resultado es que la función ha CONTADO la frecuencia de cada categoría de DemocracyIndexCat

data |>                # Data
  ggplot() +           # Iniciamos la construcción del gráfico con ggplot 
  aes(x = Democracy_Index_cat) + # Establecemos la variable como el eje x
  geom_bar()           # Creamos un gráfico de barras basado en el conteo de 'continent'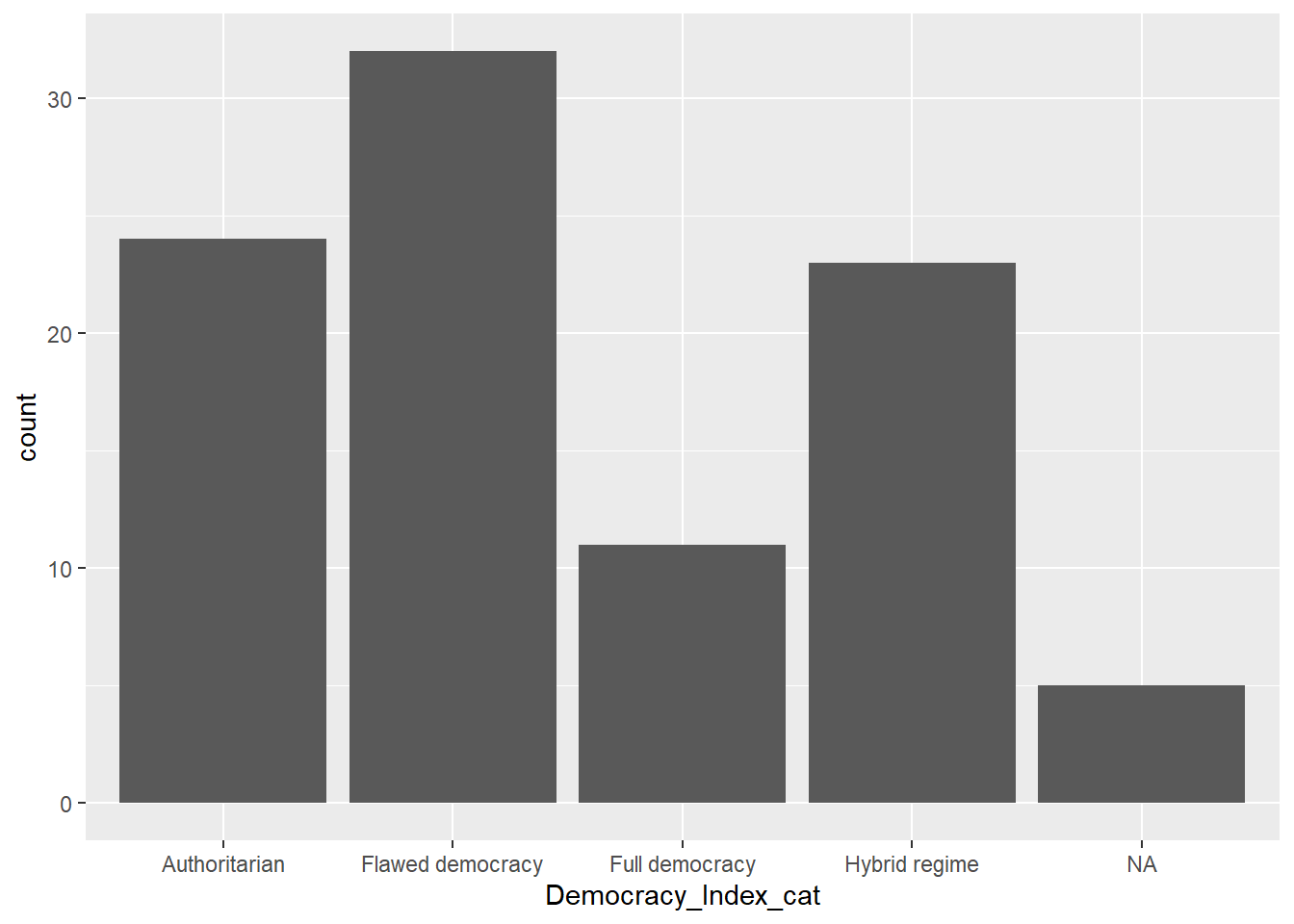

En algunas ocasiones ya contamos con el conteo realizado y sólo deseamos el gráfico. Para ello utilizamos el ARGUMENTO stat=“identity”.

Un caso como el siguiente:

data |>  
  count(Democracy_Index_cat)

# A tibble: 5 × 2
  Democracy_Index_cat     n
  <chr>               <int>
1 Authoritarian          24
2 Flawed democracy       32
3 Full democracy         11
4 Hybrid regime          23
5 <NA>                    5

En estos casos utilizamos la función:

data |>  
  count(Democracy_Index_cat) |> 
  ggplot() +           
  aes(y = n, x=Democracy_Index_cat) + #En este caso le he tenido que especificar tanto x como y!
  geom_bar(stat="identity")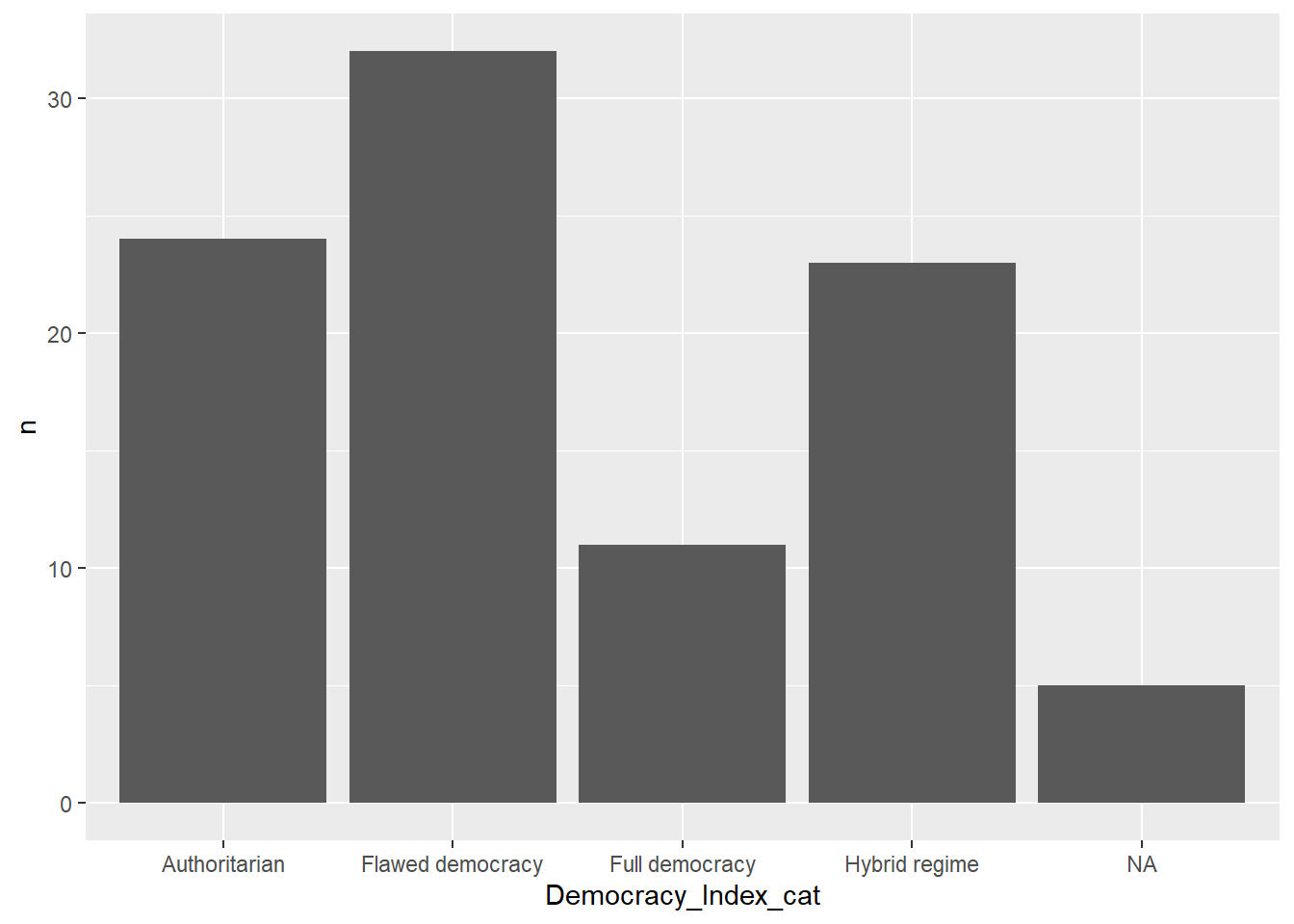          

Agregando etiquetas de los datos y nombres de los ejes:

data |>  
  count(Democracy_Index_cat) |> 
  ggplot() +           
  aes(y = n, x=Democracy_Index_cat) + #En este caso le he tenido que especificar tanto x como y!
  geom_bar(stat="identity")+
  geom_text(aes(label=n, vjust=-1, size=3))+
  labs(x="Tipo de régimen", y="Frecuencia")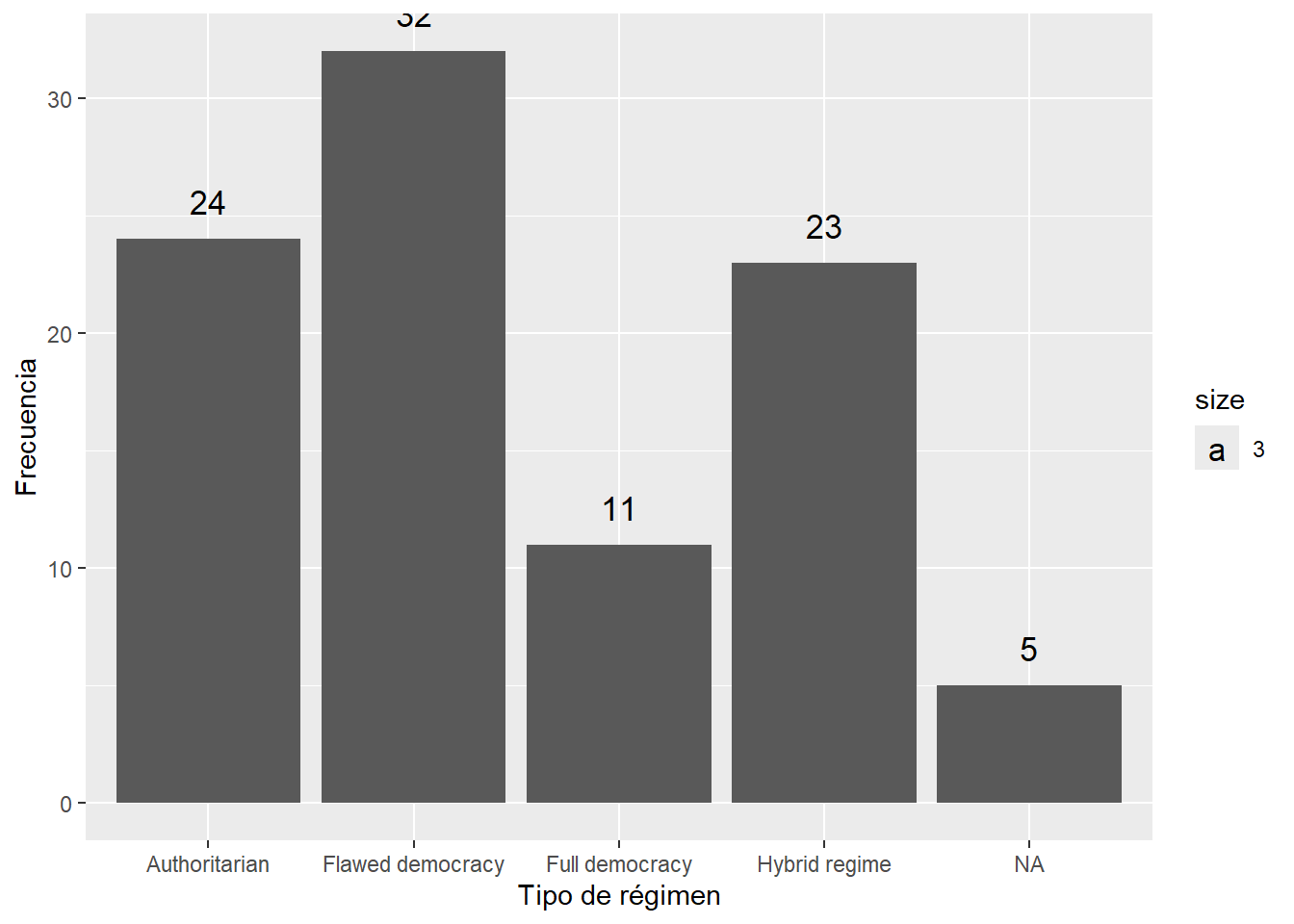

Nota

Aunque los gráficos de pie son ampliamente reconocidos y frecuentemente utilizados para mostrar proporciones de un todo, en la práctica suelen ser menos efectivos que los gráficos de barras. Esto se debe a que los gráficos de barras ofrecen una comparación más clara y precisa entre categorías, facilitando la interpretación de las diferencias en magnitud.

3.5.3 Para variables numéricas

3.5.3.1 Boxplot

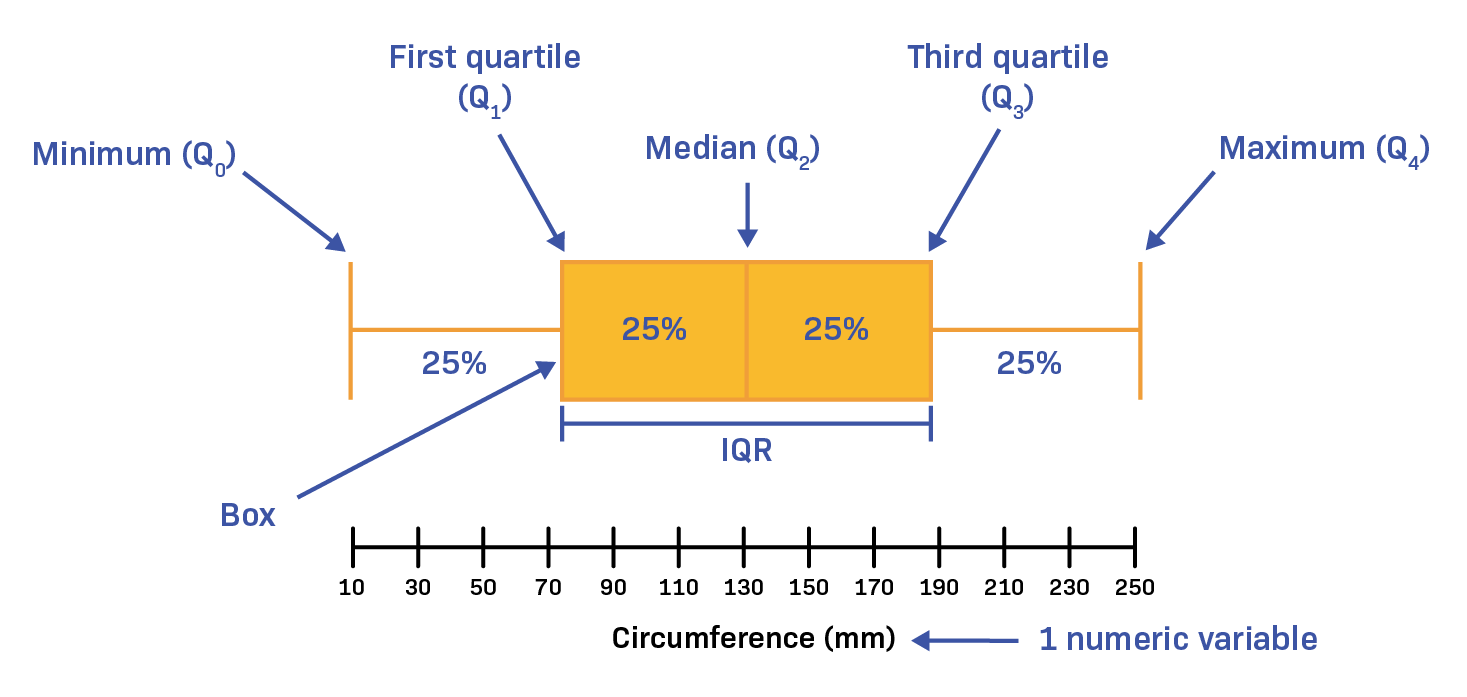
Es utilizado para representar la distribución de un conjunto de datos numéricos a través de sus cuartiles.

El gráfico consiste en una caja que representa el rango intercuartil (IQR),es decir, la diferencia entre el tercer cuartil (Q3) y el primer cuartil(Q1).

Dentro de la caja,se dibuja una línea que representa la mediana.

Los bigotes,que se extienden desde la caja, indican el rango de los datos que se encuentran dentro de un cierto múltiplo del IQR, generalmente 1.5 veces el IQR.

data |> 
  ggplot() + 
  aes(y = PBIPC) + # Establecemos 'lifeExp' en el eje x
  geom_boxplot()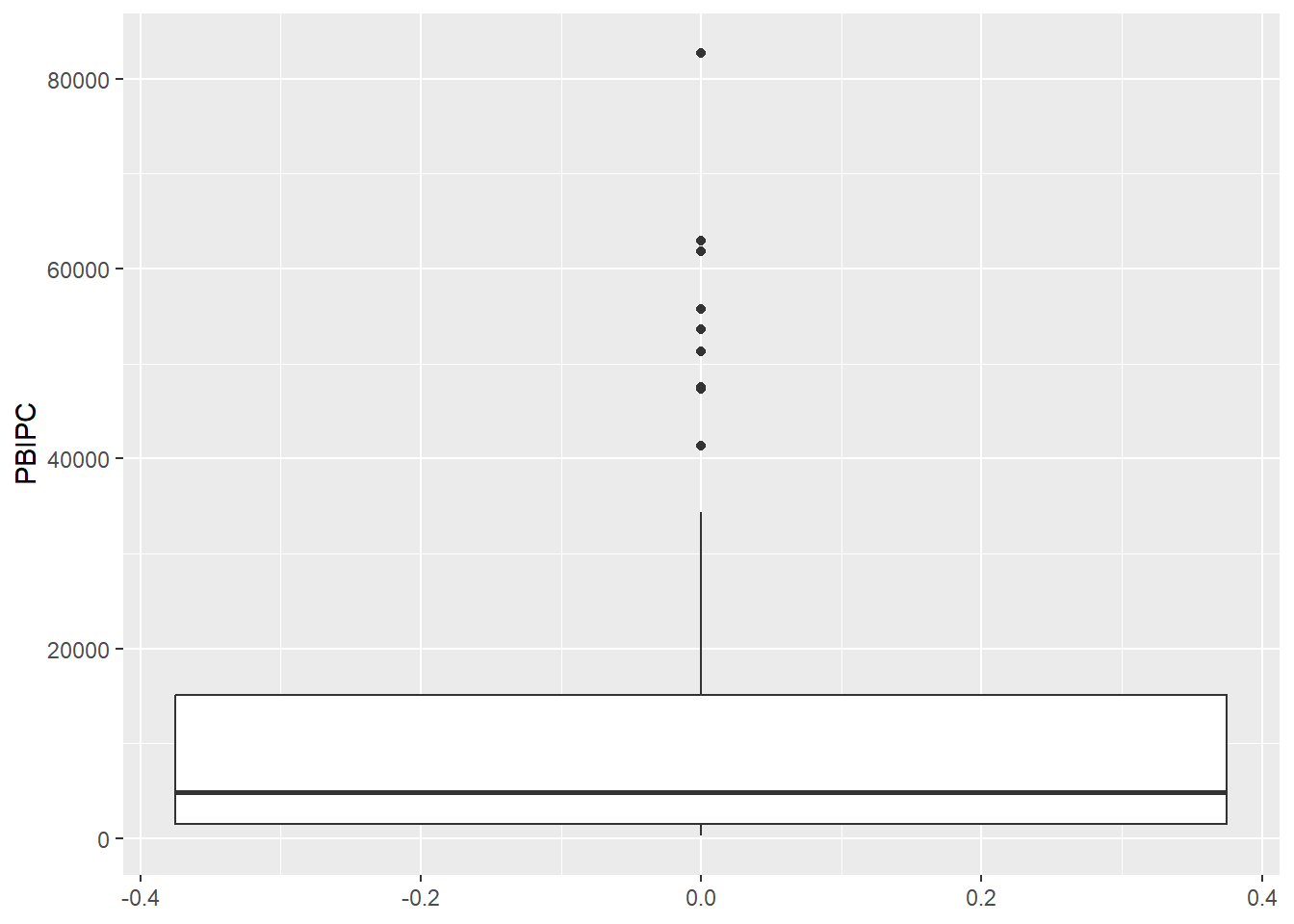

Los valores que están por encima o por debajo de los bigotes se representan como puntos o asteriscos, que se conocen como valores atípicos.

El boxplot es útil para identificar valores atípicos y para comparar la distribución de varios conjuntos de datos en un solo gráfico. También permite visualizar la simetría o asimetría de la distribución y la presencia de sesgo.

Puedes probar este video sugerido:

También puedes solicitar boxplot por grupos:

data |> 
  ggplot() + 
  aes(y = PBIPC, colour=Continent) + # Establecemos 'lifeExp' en el eje x
  geom_boxplot()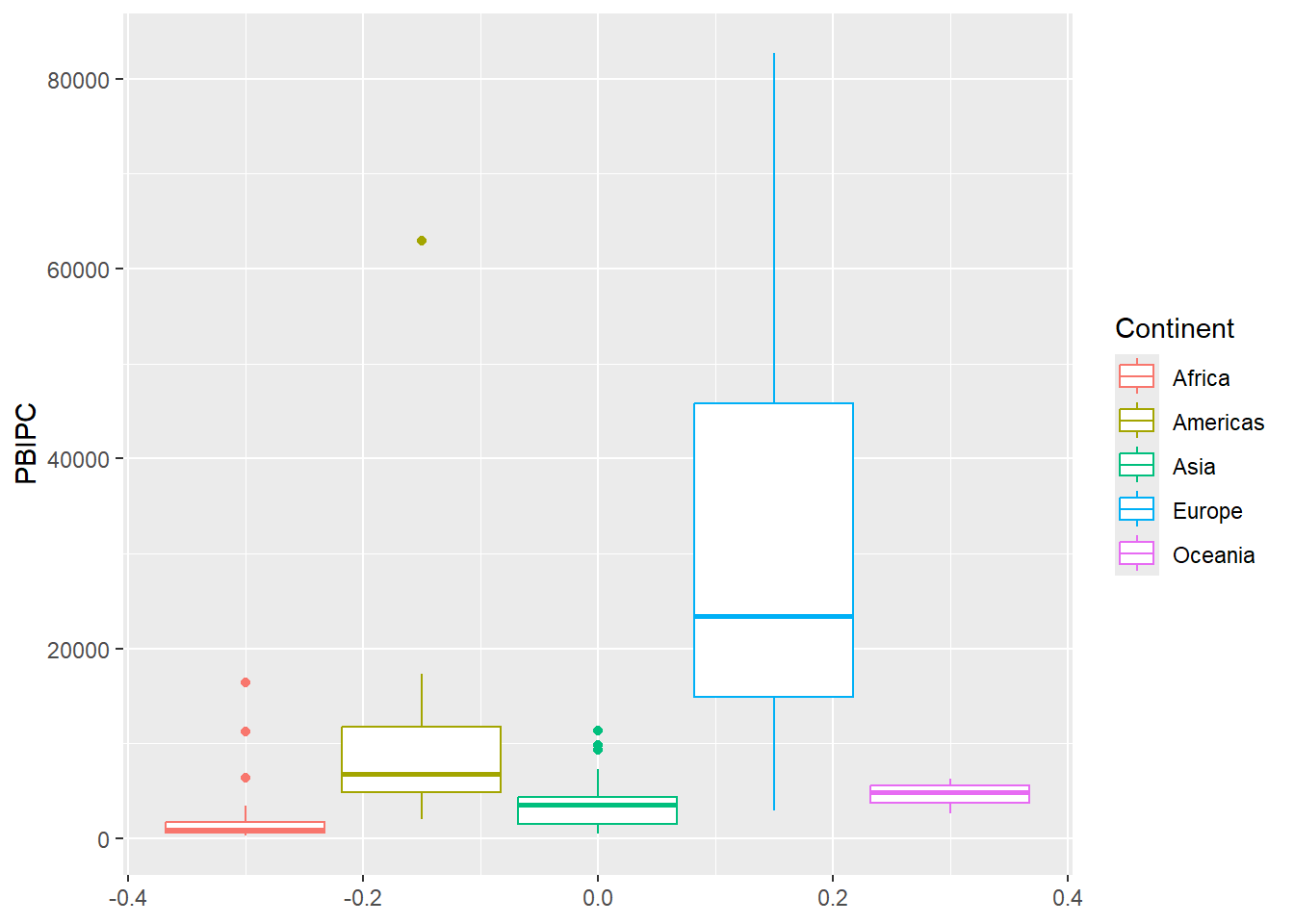

¿qué nos dice este gráfico?

3.5.3.2 Histograma

Un histograma es un tipo de gráfico utilizado en estadísticas para representar la distribución de un conjunto de datos numéricos mediante barras. Cada barra en un histograma representa la frecuencia (número de veces que ocurren) de datos dentro de un intervalo o “bin” específico.

Los bins dividen el espectro completo de los datos en series de intervalos consecutivos, y son todos de igual tamaño. La altura de cada barra muestra cuántos datos caen dentro de cada intervalo.

data |> 
  ggplot() + 
  aes(x=PBIPC) + 
  geom_histogram()

`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.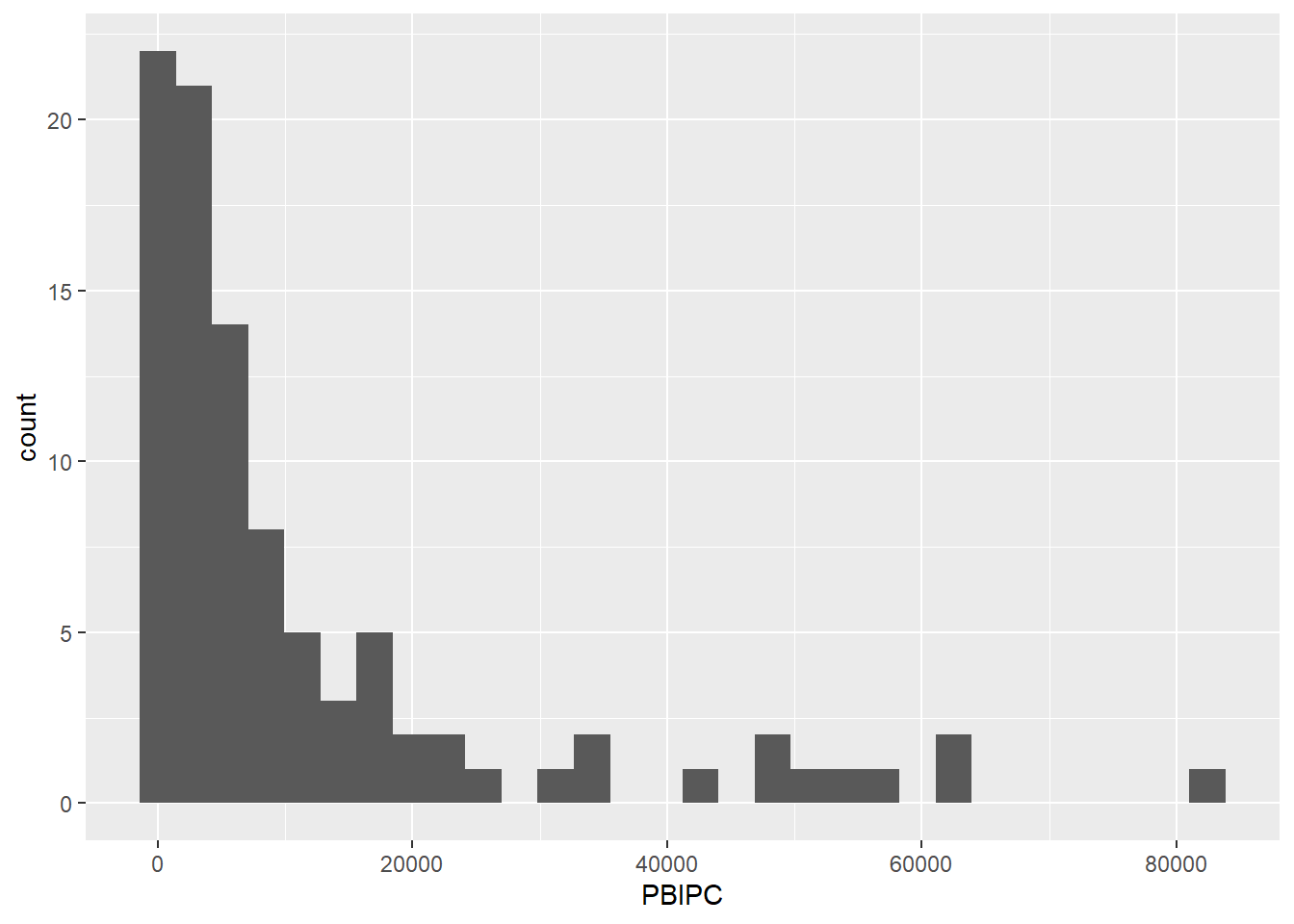

Los histogramas permiten observar cómo se distribuyen los datos, revelando si están equilibradamente repartidos o inclinados hacia un extremo. Una distribución es simétrica cuando las mitades a ambos lados de la media son imágenes espejo.

Si está sesgada hacia la derecha, significa que hay una acumulación de datos hacia el lado izquierdo del gráfico, con una cola que se extiende hacia la derecha. Como en el caso del gráfico de líneas arriba.

Por otro lado, un sesgo hacia la izquierda indica una concentración de datos hacia la derecha, con una cola que se alarga hacia la izquierda. Los histogramas también muestran si los datos se agrupan en torno a varios valores centrales, evidenciado por la presencia de varios picos o “modas”.

Así como nuestros gráficos anteriores, podemos personalizar mucho más nuestro gráfico:

data |> 
  ggplot() + 
  aes(x=PBIPC) + 
  geom_histogram()+
  geom_vline(xintercept = mean(data$PBIPC), color = "red")+
  geom_vline(xintercept = median(data$PBIPC), color = "green")

`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.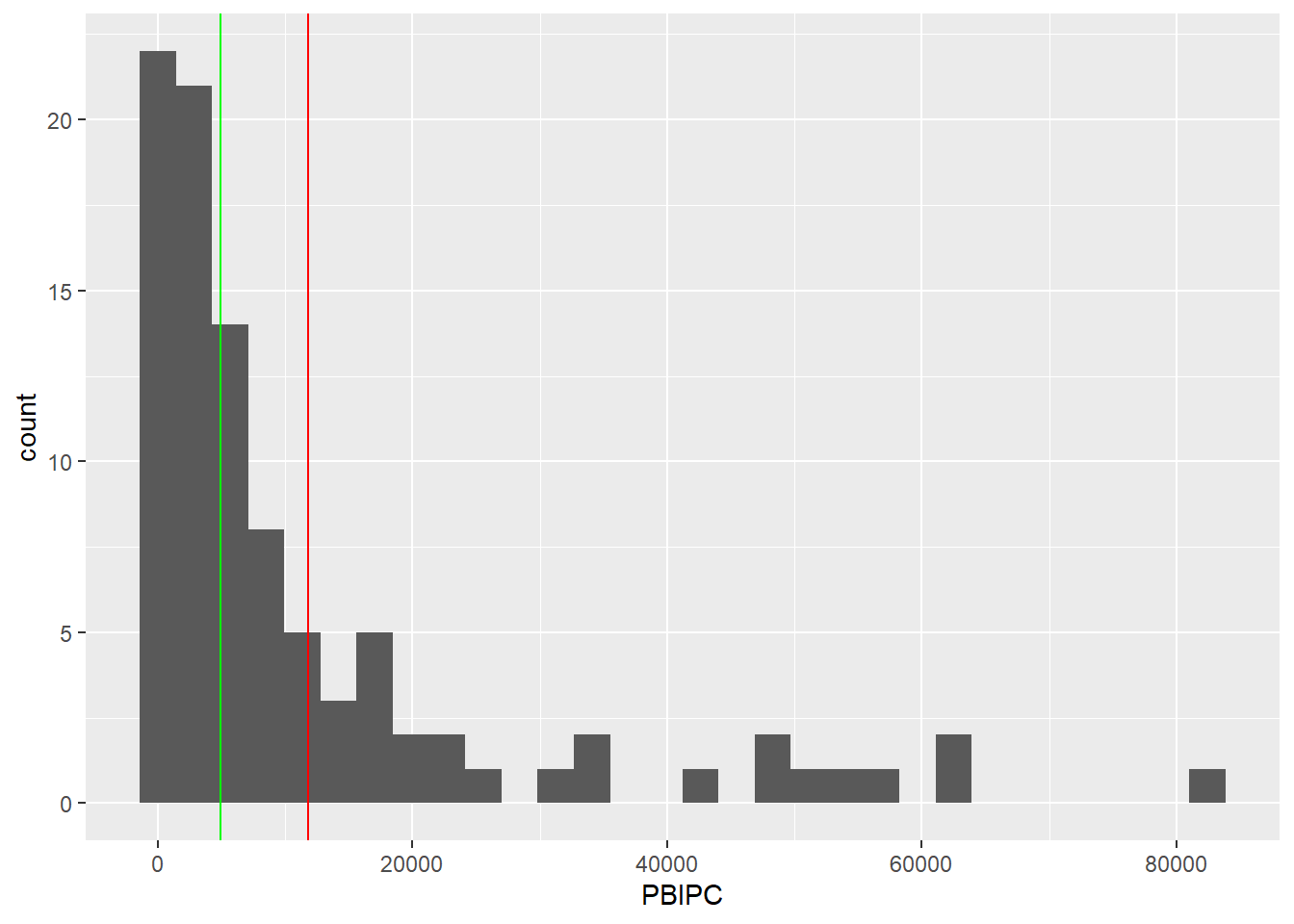

3.5.3.3 Gráfico de línea

El gráfico de líneas es una herramienta de visualización de datos que conecta puntos de datos individuales con líneas, mostrando tendencias o cambios en una variable numérica a lo largo del tiempo o de otra variable numérica. Sirve principalmente para visualizar la evolución de una o varias cantidades, permitiendo identificar patrones, tendencias, picos, y caídas en los datos a lo largo de un período o rango específico.

library(readxl)
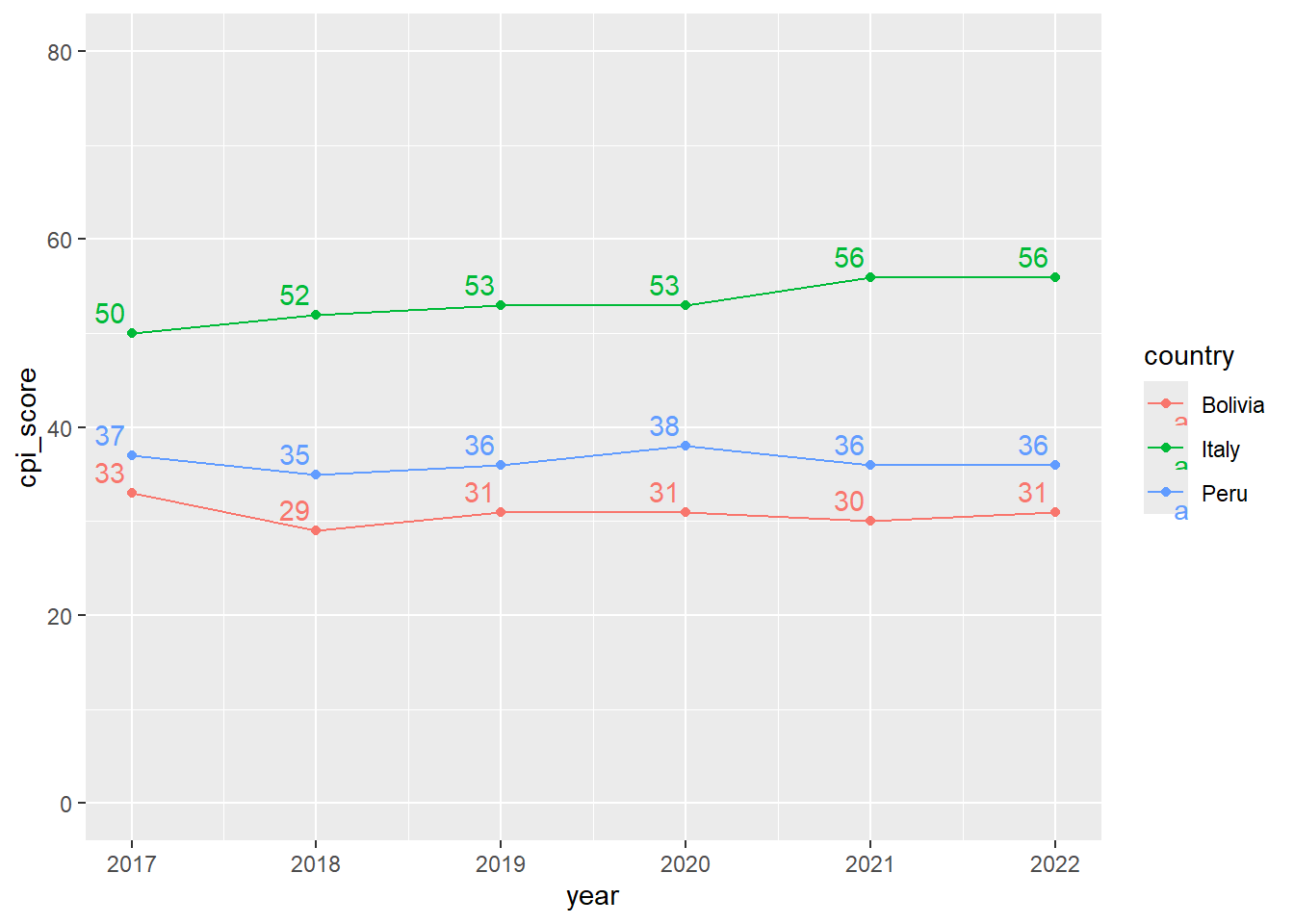
CPI<-read_xlsx("data/CPI.xlsx")

Cómo evolucionó Perú en el CPI score desde el 2017?

CPI |> 
  filter(country=="Peru"|country=="Bolivia" |country=="Italy") |> 
  ggplot() +
  aes(x=year, y=cpi_score, color=country)+
  geom_line()+
  geom_point()+
  ylim(0, 80)+
  geom_text(aes(label=round(cpi_score, 1)), 
            vjust=-0.5,                   
            hjust=1.2)