Capítulo 5 Análisis exploratorio de datos

Como sabemos, los estadísticos de tendencia central van a depender del tipo de variable que estemos analizando.

Para practicar este apartado vamos a utilizar la base de datos de Lapop del año 2017. Lapop es el Proyecto de Opinión Pública de América Latina implementado por la Universidad de Vanderbilt, el cual es un proyecto de investigación multinacional especializado en el desarrollo, implementación y análisis de encuestas de opinión pública.

Abrimos la base de datos desde nuestro repositorio:

library(rio)
link="https://github.com/DataPolitica/salidas/raw/master/Data/sub_lapop.sav"
lapop=import(link)

Esta base de datos ha sido editada con fines didácticos (idioma, recodificación, etc).

5.1 Para nominales

5.1.1 Preparación

Selecciones la variable urbanorural y procedemos a configurarla adecuadamente.

Primero identifiquemos cómo el R está leyendo la variable.

str(lapop$urbanorural)

##  num [1:2153] 2 2 2 2 2 2 2 2 2 2 ...
##  - attr(*, "label")= chr "Urbano / Rural"
##  - attr(*, "format.spss")= chr "F8.2"
##  - attr(*, "display_width")= int 9
##  - attr(*, "labels")= Named num [1:2] 1 2
##   ..- attr(*, "names")= chr [1:2] "Urbano" "Rural"

class(lapop$urbanorural)

## [1] "numeric"

Luego, al ver que aún se encuentra como numérico, entonces lo convertimos en factor:

lapop$urbanorural=as.factor(lapop$urbanorural)
class(lapop$urbanorural)

## [1] "factor"

Verificamos los niveles y, de acuerdo con la metadata, le asignamos las etiquetas a cada uno de los mismos.

levels(lapop$urbanorural)

## [1] "1" "2"

levels(lapop$urbanorural)<-c("Urbano","Rural")
levels(lapop$urbanorural)

## [1] "Urbano" "Rural"

Asimismo, podemos solicitar una tabla que nos muestre las proporciones por cada categoría. Para ello, utilizamos la función prop.table(). Cuando escribimos esta función hay que tener en cuenta que la tenemos que aplicar sobre la tabla de frecuencias normal (que aplicamos anteriormente):

prop.table(table(lapop$urbanorural))

## 
##    Urbano     Rural 
## 0.6149559 0.3850441

Si queremos los porcentaje hacemos lo mismo pero al final le decimos que lo multiple por 100 (*100):

prop.table(table(lapop$urbanorural))*100

## 
##   Urbano    Rural 
## 61.49559 38.50441

Ya tenemos la variable lista para aplicar técnicas de análisis descriptivo.

5.1.2 Estadísticos descriptivos

Lo primero que podemos hacer es solicitar la función summary. Esta función nos va a dar una mirada rápida al contenido de nuestra variable. En el caso de ser factor, nos va a mostrar las frecuencias (incluye los NA si los hubiera):

summary(lapop$urbanorural)

## Urbano  Rural 
##   1324    829

Como sabemos el estadístico más idóneo para variables nominales es la moda. Por ello, hacemos uso del paquete DescTools y de la función Mode():

library(DescTools)
Mode(lapop$urbanorural)

## [1] Urbano
## attr(,"freq")
## [1] 1324
## Levels: Urbano Rural

Lo que nos dice el resultado es que la moda es la categoría Urbano y nos indica la frecuencia.

Otra opción también es solicitar una tabla simple para ver la frecuencia de cada categoría.

table (lapop$urbanorural)

## 
## Urbano  Rural 
##   1324    829

5.1.3 Gráficos

Lo primero que podemos solicitar es un diagrama de pie o de sectores. Nótese que primero debemos crear un objeto que sea la tabla de la variable que deseamos graficar, en este caso, de urbano rural. De esa manera, el programa podrá utilizar los datos y plasmarlos en un gráfico.

mi_tabla <- table(lapop$urbanorural)
pie(mi_tabla)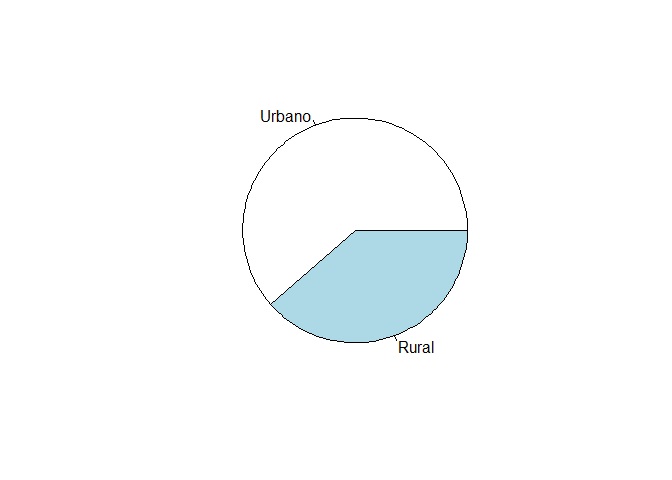

Image

Es recomendable graficar un máximo de 7 sectores. Si colocamos una varaible con más sector puede resultar confusa la interpretación.

También podemos solicitar un diagrama de barras.

barplot(mi_tabla)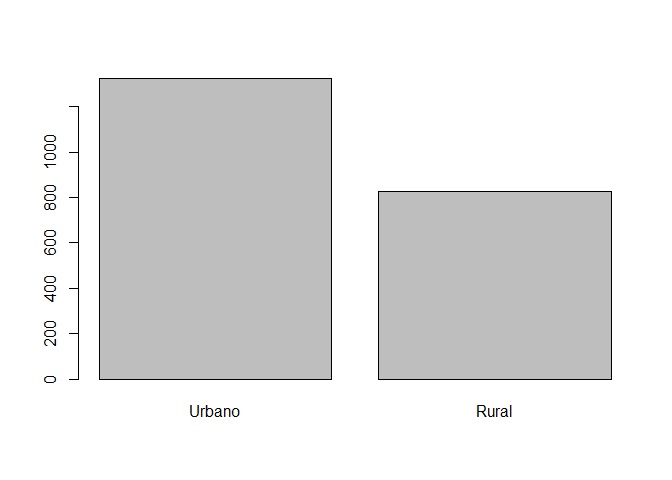

Image

Agregando más detalles a nuestros gráficos

Hasta este momento hemos visto que podemos solicitar gráficos de una forma muy práctica. Sin embargo, nosotros podemos solicitar un producto más elaborado en la medida en que agreguemos más características al código.

Por ejemplo, si deseamos un diagrama de barras azul escribimos:

barplot(mi_tabla, col="blue")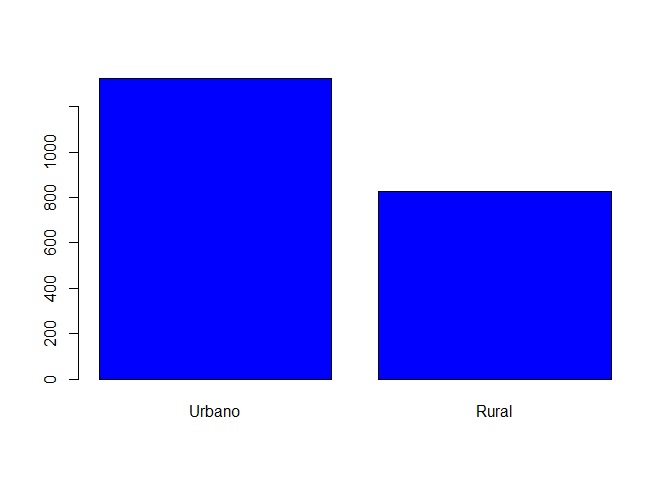

Image

Si deseamos un diagrama de barras azul y con título escribimos:

barplot(mi_tabla,col="blue", 
        main="Casos según su lugar de procedencia")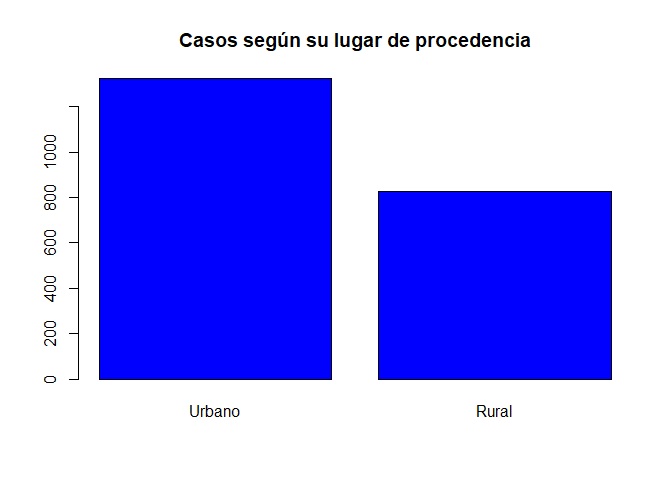

Image

Como nos damos cuenta, nosotros podemos ir agregando más características a nuestro código. Es posible que recuerdes ejemplos de códigos de programación que son líneas interminables. Eso es así porque los programadores elaboran productos muy específicos y que, en su mayoría de veces, requieren la especificación de muchas características.

Nuestro objetivo será avanzar en el uso de estos códigos de programación para poder, al igual que los programadores, elaborar análisis estadísticas cada vez más complejos y específicos.

5.2 Para ordinales

Abrimos la base de datos LAPOP desde nuestro repositorio:

library(rio)
link="https://github.com/DataPolitica/salidas/raw/master/Data/sub_lapop.sav"
lapop=import(link)

5.2.1 Preparación

Esta vez vamos a utilizar la variable Interés en la política. Procedemos a configurarla adecuadamente.

Primero identifiquemos cómo el R está leyendo la variable.

str(lapop$interes)

##  num [1:2153] 2 2 1 1 1 2 2 2 2 3 ...
##  - attr(*, "label")= chr "Interés en la política"
##  - attr(*, "format.spss")= chr "F8.2"
##  - attr(*, "display_width")= int 11
##  - attr(*, "labels")= Named num [1:4] 1 2 3 4
##   ..- attr(*, "names")= chr [1:4] "Nada" "Un poco" "Algo" "Mucho"

class(lapop$interes)

## [1] "numeric"

Luego, al ver que aún se encuentra como numérico, entonces lo convertimos en factor ordenado:

lapop$interes=ordered(lapop$interes)
class(lapop$interes)

## [1] "ordered" "factor"

Verificamos los niveles y, de acuerdo con la metadata, le asignamos las etiquetas a cada uno de los mismos. En este caso los significados son: 1, “Nada”; 2, “Poco”; 3, “Algo”; y 4, “Mucho”.

levels(lapop$interes)

## [1] "1" "2" "3" "4"

levels(lapop$interes)<-c("Nada","Poco", "Algo", "Mucho")
levels(lapop$interes)

## [1] "Nada"  "Poco"  "Algo"  "Mucho"

Ya tenemos la variable lista para aplicar técnicas de análisis descriptivo para ordinales.

5.2.2 Estadísticos descriptivos

Al igual que la sección anterior, podemos solicitar la función summary() para que nos muestre las frecuencias por cada categoría (en este caso tampoco tenemos NA´´s):

summary(lapop$interes)

##  Nada  Poco  Algo Mucho 
##   632   787   532   202

Utilizando el paquete DescTools podemos solicitar la moda, con la función Mode(); y la mediana, con la función Median():

library(DescTools)
Mode(lapop$interes)

## [1] Poco
## attr(,"freq")
## [1] 787
## Levels: Nada < Poco < Algo < Mucho

Median(lapop$interes)

## [1] Poco
## Levels: Nada < Poco < Algo < Mucho

Lo que nos dice el resultado es que la moda es la categoría Poco. La mediana nos dice que, si ordenamos los resultados de menor a mayor, el valor central es Poco. También podemos interpretarlo como que “al menos el 50% de los casos tienen poco interés en la política”.

Otra opción, al igual que las nominales, es solicitar una tabla simple para ver la frecuencia de cada categoría.

table (lapop$interes)

## 
##  Nada  Poco  Algo Mucho 
##   632   787   532   202

5.2.3 Gráficos

Primero creamos un objeto que sea la tabla de la variable que deseamos graficar, en este caso, interés por la política.

mi_tabla <- table(lapop$interes)
mi_tabla

## 
##  Nada  Poco  Algo Mucho 
##   632   787   532   202

Solicitamos un diagrama de pie o sector con la función pie():

pie(mi_tabla)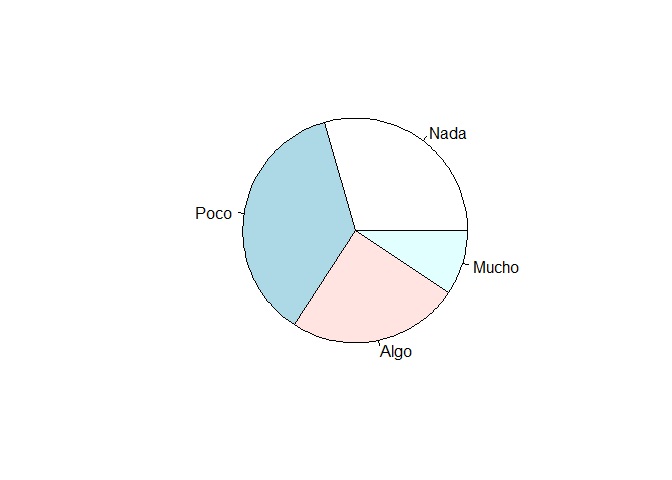

Image

Solicitamos un diagrama de barras con la función barplor():

barplot(mi_tabla)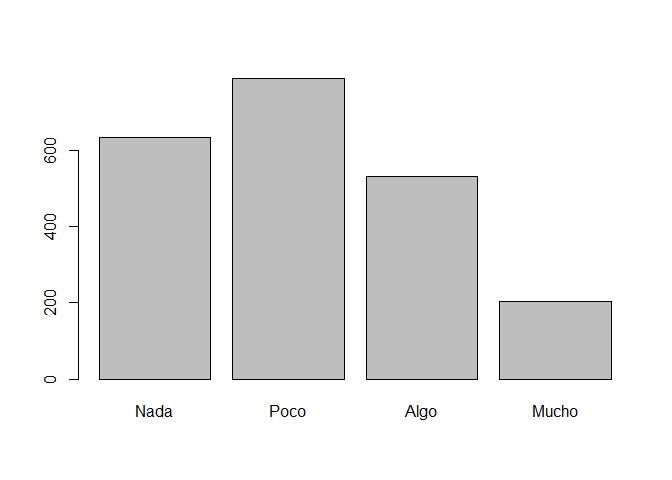

Image

5.3 Para numéricas

5.3.1 Preparación

Abrimos la base de datos LAPOP desde nuestro repositorio:

library(rio)
link="https://github.com/DataPolitica/salidas/raw/master/Data/sub_lapop.sav"
lapop=import(link)

Seleccionamos la variable ingresos

5.3.2 Estadísticos descriptivos

Solicitar la función summary() y vamos a ver que el resultado variable significativamente de los resultados de las variables categóricas:

summary(lapop$ingresos)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##    1316    2661    3010    3012    3341    4667

Como vemos, el summary ahora nos muestra los principales estadísticos de una variable numérica, es decir: mínimo, 1er cuartil, mediana, media o promedio, 3er cuartil y máximo. Siempre que tengamos una variable numérica comencemos por solicitar esta función.

5.3.3 Estadísticos de dispersión

La lógica es la misma, colocamos la función y entre paréntesis el nombre de la variable:

Si deseamos la desviación estándar utilizamos la función sd():

sd(lapop$ingresos)

## [1] 498.6063

Si deseamos la varianza utilizamos la función var():

var(lapop$ingresos)

## [1] 248608.3

También podemos pedir estadísticos de dispersión.

Para solicitar la asimetría y curtosis primero abrimos el paquete e1071:

library(e1071)

Para la asimetría utilizamos la función skewness():

skewness(lapop$ingresos)

## [1] 0.0544436

Para la curtosis utilizamos la función kurtosis():

kurtosis(lapop$ingresos)

## [1] -0.0678835

5.3.4 Gráficos

En este caso, como estamos ante una variable numérica, no necesitamos crear una tabla antes de solicitar los gráficos.

Histograma

Solicitemos un histograma con la función hist():

hist(lapop$ingresos)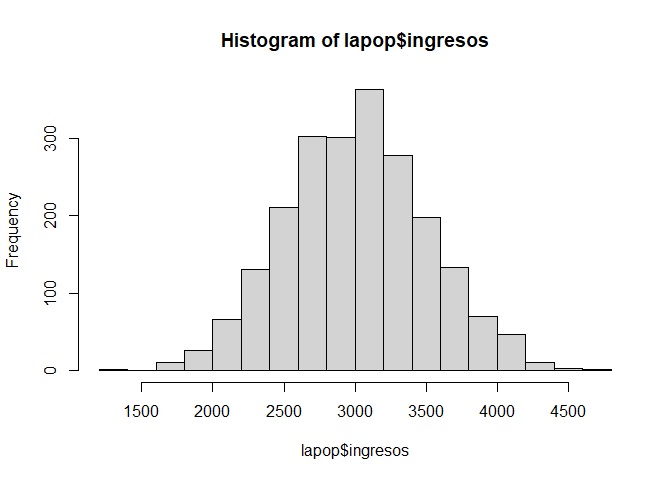

Image

Diagrama de cajas o boxplot

Solicitemos un diagrama de cajas con la función boxplot():

boxplot(lapop$ingresos)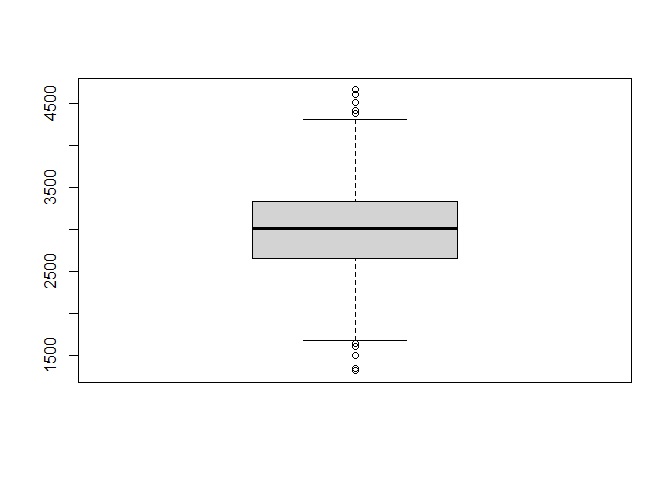

Image

5.4 Análisis bivariado

5.4.1 Tablas de contingencia

Abrimos la base de datos LAPOP desde nuestro repositorio:

library(rio)
link="https://github.com/DataPolitica/salidas/raw/master/Data/sub_lapop.sav"
lapop=import(link)

Verificamos y configuramos adecuadamente las variables que utilizaremos

lapop$urbanorural=as.factor(lapop$urbanorural)
levels(lapop$urbanorural)<-c("Urbano","Rural")
lapop$sexo=as.factor(lapop$sexo)
levels(lapop$sexo)<-c("Hombre","Mujer")

Una vez que hemos identificamos dos variables categóricas lo primeros que podemos solicitar es una tabla de contingencia.

Ante de seguir te sugiero ver el siguiente tutorial para solicitar tablas de contigencias:

Como vimos en el video, podemos pedir tablas de contingencia con la función table(). Hagamos una tabla para las variables urbanorural y sexo:

Primero hallemos una tabla de contingencia simple, con sólo las frecuencias. La llamaremos tabla1:

tabla1 <- table(lapop$urbanorural, lapop$sexo)
tabla1

##         
##          Hombre Mujer
##   Urbano    687   637
##   Rural     434   395

Podemos agregarle los totales marginales escribiendo la siguiente función addmargins()

addmargins(tabla1)

##         
##          Hombre Mujer  Sum
##   Urbano    687   637 1324
##   Rural     434   395  829
##   Sum      1121  1032 2153

Ahora, pidamos una tabla de contingencia con porcentaje Tenemos que hacer referencia a la tabla creada anteriormente y usar el comando prop.table() y lo multiplicamos por 100. La llamaremos tabla2:

tabla2 <- prop.table(tabla1)*100
tabla2

##         
##            Hombre    Mujer
##   Urbano 31.90896 29.58662
##   Rural  20.15792 18.34649

Vemos que nos da los valores totales, pero nosotros queremos sólo los porcentaje por columna. Para ello, debemos hacer referencia a las columnas dentro del comando agregando el número 2 (si ponemos 1 aparecerán los porcentaje por filas)

tabla3 <- prop.table(tabla1, 2)*100
tabla3

##         
##            Hombre    Mujer
##   Urbano 61.28457 61.72481
##   Rural  38.71543 38.27519

Por último, podemos agregarle los totales marginales escribiendo la siguiente función addmargins()

addmargins(tabla3)

##         
##             Hombre     Mujer       Sum
##   Urbano  61.28457  61.72481 123.00937
##   Rural   38.71543  38.27519  76.99063
##   Sum    100.00000 100.00000 200.00000

5.4.2 Una numérica y una categórica

Para mostrar los descriptivos de una variable numérica según una variable categórica tenemos que considerar a esta última como grupos. De esta manera, lo que hacemos en realidad es la comparación de la numérica entre 2 o más grupos.

Para ello, utilizamos el paquete psych()

library(psych)

Para describir la varible podemos utilizar la función describeBy(). Notemos que primero debemos poner la variable numérica y luego el grupo de comparación.

Por ejemplo, obtengamos los estadísticos descriptivos de la variable Edad según si la persona pertenece al ámbito rural o urbano (categórica/grupos):

describeBy(lapop$edad,group=lapop$urbanorural)

## 
##  Descriptive statistics by group 
## group: Urbano
##    vars    n  mean    sd median trimmed   mad min max range skew kurtosis  se
## X1    1 1324 37.79 14.59     35   36.51 14.83  18  86    68 0.67    -0.27 0.4
## ------------------------------------------------------------ 
## group: Rural
##    vars   n  mean    sd median trimmed   mad min max range skew kurtosis   se
## X1    1 829 36.96 13.68     35   35.84 14.83  18  80    62 0.63    -0.25 0.48

También podemos solicitar un diagrama de cajas o boxplot según los grupos:

boxplot(lapop$edad~lapop$urbanorural)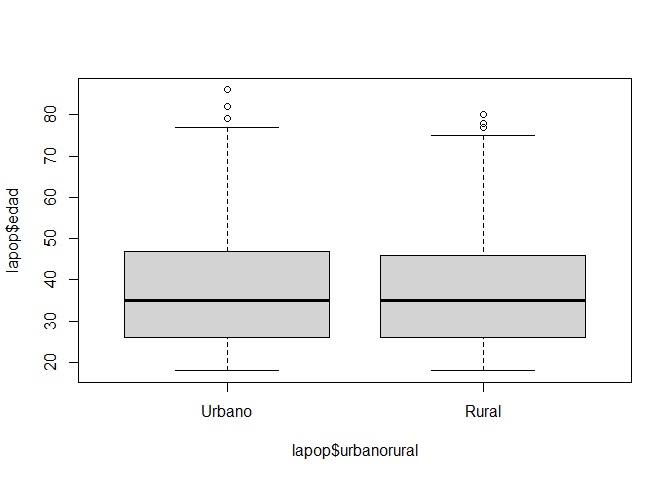

Image

5.4.3 Dos variables numéricas

Utilicemos la base de datos trabajadores:

library(rio)
base_trabajadores="https://github.com/DataPolitica/salidas/raw/master/Data/trabajadores.sav"
trabajadores=import(base_trabajadores)

Para analizar la relación entre dos variables numéricas es muy común referirse al gráfico de dispersión.

Para ello, solicitamos el gráfico con la función plot(). Entre paréntesis colocar las dos variables numéricas: el salario inicial y el salario actual de los trabajadores de una empresa.

plot(trabajadores$salario_actual, trabajadores$salario_inicial)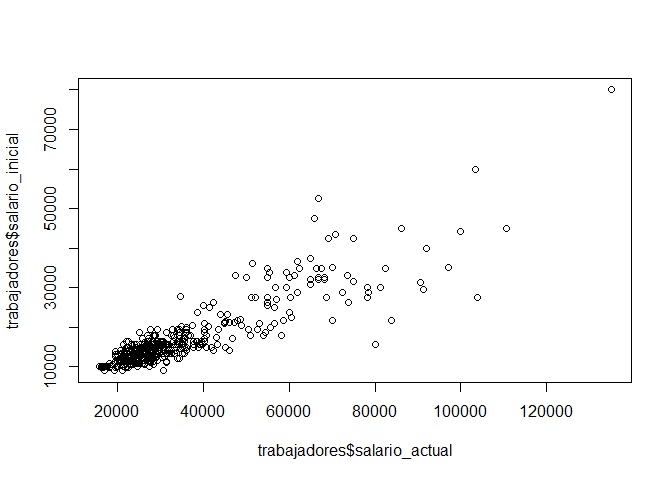

Image

Podemos especificar más elementos de nuestro gráfico de dispersión. Agreguemos título del gráfico y etiquetas de los ejes X e Y:

plot(trabajadores$salario_actual, trabajadores$salario_inicial, 
     main="Relación entre salario inicial y salario final", 
     xlab="Salario actual", 
     ylab="Salario final")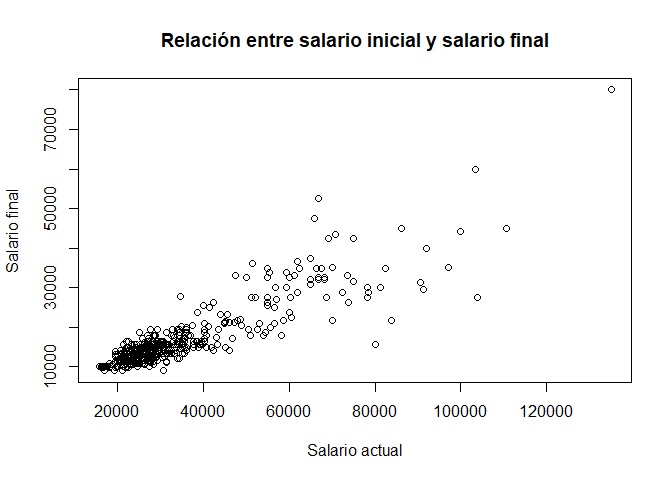

Image